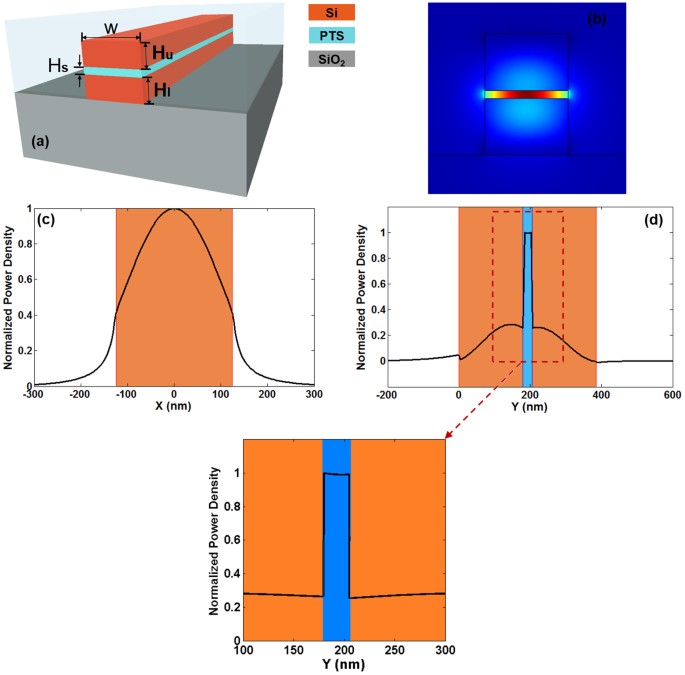
The effective index variation of the guided mode for a Si 3 N 4 /SiO 2 multiple (triple)-slot structure as a function of the bulk (fluid) refractive index variation has been estimated to be improved by 20% as compared to that of a single-slot waveguide. This is a consequence of a larger localization of the E-field of the propagating optical. Abstract:Slot waveguides allow for high optical confinement in a planar optical waveguide. Here we show a method for maintaining this high degree of confinement in slot waveguides with sharp bends. This high confinement can be achieved by using an asymmetric slot-based structure, where the mode in the bend remains localized in the slot region. The proposed slot waveguide consists of a vertical slot structure placed above a silicon slab, with a low- index buffer layer between them to construct a T-shaped slot region. Such a T-shaped slot waveguide could be realized by using similar fabrication methods of the conventional slot waveguides. The proposed slot waveguide consists of a vertical slot structure placed above a silicon slab, with a low- index buffer layer between them to construct a T-shaped slot region. Such a T-shaped slot waveguide could be realized by using similar fabrication methods of the conventional slot waveguides.

A slot-waveguide is an optical waveguide that guides strongly confined light in a subwavelength-scale low refractive index region by total internal reflection.

A slot-waveguide consists of two strips or slabs of high-refractive-index (n_H) materials separated by a subwavelength-scale low-refractive-index (n_S) slot region and surrounded by low-refractive-index (n_C) cladding materials.

Principle of operation[edit]

The principle of operation of a slot-waveguide is based on the discontinuity of the electric field (E-field) at high-refractive-index-contrast interfaces. Maxwell’s equations state that, to satisfy the continuity of the normal component of the electric displacement fieldD at an interface, the corresponding E-field must undergo a discontinuity with higher amplitude in the low-refractive-index side. That is, at an interface between two regions of dielectric constants ε_S and ε_H, respectively:

D_S^N=D_H^N

ε_SE_S^N=ε_HE_H^N

n_S²E_S^N=n_H²E_H^N

where the superscript N indicates the normal components of D and E vector fields. Thus, if n_S<<n_H, then E_S^N>>E_H^N.

Given that the slot critical dimension (distance between the high-index slabs or strips) is comparable to the exponential decay length of the fundamental eigenmode of the guided-wave structure, the resulting E-field normal to the high-index-contrast interfaces is enhanced in the slot and remains high across it. The power density in the slot is much higher than that in the high-index regions. Since wave propagation is due to total internal reflection, there is no interference effect involved and the slot-structure exhibits very low wavelength sensitivity.^[1]

Invention[edit]

The slot-waveguide was born in 2003 as an unexpected outcome of theoretical studies on metal-oxide-semiconductor (MOS) electro-opticmodulation in high-confinement silicon photonic waveguides by Vilson Rosa de Almeida and Carlos Angulo Barrios, then a Ph.D. student and a Postdoctoral Associate, respectively, at Cornell University. Theoretical analysis ^[1] and experimental demonstration ^[2] of the first slot-waveguide implemented in the Si/SiO₂ material system at 1.55 μm operation wavelength were reported by Cornell researchers in 2004.

Since these pioneering works, several guided-wave configurations based on the slot-waveguide concept have been proposed and demonstrated. Relevant examples are the following:

In 2005, researchers at the Massachusetts Institute of Technology proposed to use multiple slot regions in the same guided-wave structure (multi-slot waveguide) in order to increase the optical field in the low-refractive-index regions.^[3] The experimental demonstration of such multiple slot waveguide in a horizontal configuration was first published in 2007.^[4]

In 2006, the slot-waveguide approach was extended to the terahertz frequency band by researchers at RWTH Aachen University.^[5] Researchers at the California Institute of Technology also demonstrated that a slot waveguide, in combination with nonlinear electrooptic polymers, could be used to build ring modulators with exceptionally high tunability.^[6] Later this same principle enabled Baehr-Jones et al. to demonstrate a mach-zehnder modulator with an exceptionally low drive voltage of 0.25 V^[7][8]

In 2007, a non-planar implementation of the slot-waveguide principle of operation was demonstrated by researchers at the University of Bath. They showed concentration of optical energy within a subwavelength-scale air hole running down the length of a photonic-crystal fiber.^[9]

Recently, in 2016, it is shown ^[10] that slots in a pair of waveguides if off-shifted away from each other can enhance the coupling coefficient even more than 100% if optimized properly, and thus the effective power coupling length between the waveguides can significantly be reduced. Hybrid slot (having vertical slot in one waveguide and horizontal slot in the other) assisted polarization beam splitter is also numerically demonstrated. Though, the losses are high for such slot structures, this scheme exploiting the asymmetric slots may have potential to design very compact optical directional couplers and polarization beam splitters for on-chip integrated optical devices.

The slot waveguide bend is another structure essential to the waveguide design of several Integrated micro- and nano-optics devices. One of the benefits of waveguide bends is the reduction of the footprint size of the device. There are two approaches based on the similarity of Si rails width to form the sharp bend in slot waveguide, which are the symmetric and asymmetric slot waveguides ^[11].

Fabrication[edit]

Slot Waveguide Modulator

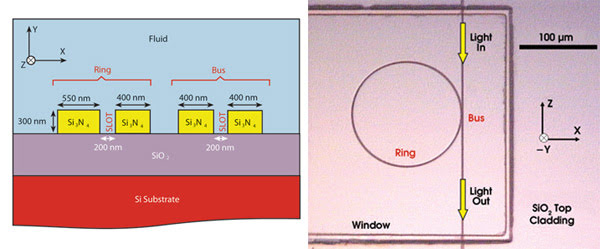
Planar slot-waveguides have been fabricated in different material systems such as Si/SiO₂^[2][12][13] and Si₃N₄/SiO₂.^[14] Both vertical (slot plane is normal to the substrate plane) and horizontal (slot plane is parallel to the substrate plane) configurations have been implemented by using conventional micro- and nano-fabrication techniques. These processing tools include electron beam lithography, photolithography, chemical vapour deposition [usually low-pressure chemical vapour deposition (LPCVD) or plasma enhanced chemical vapour deposition (PECVD)], thermal oxidation, reactive-ion etching and focused ion beam.

In vertical slot-waveguides, the slot and strips widths are defined by electron- or photo-lithography and dry etching techniques whereas in horizontal slot-waveguides the slot and strips thicknesses are defined by a thin-film deposition technique or thermal oxidation. Thin film deposition or oxidation provides better control of the layers dimensions and smoother interfaces between the high-index-contrast materials than lithography and dry etching techniques. This makes horizontal slot-waveguides less sensitive to scattering optical losses due to interface roughness than vertical configurations.

Fabrication of a non-planar (fiber-based) slot-waveguide configuration has also been demonstrated by means of conventional microstructured optical fiber technology.^[9]

Slot Waveguide Modes

Applications[edit]

A slot-waveguide produces high E-field amplitude, optical power, and optical intensity in low-index materials at levels that cannot be achieved with conventional waveguides. This property allows highly efficient interaction between fields and active materials, which may lead to all-optical switching,^[15]optical amplification^[16][17] and optical detection ^[6] on integrated photonics. Strong E-field confinement can be localized in a nanometer-scale low-index region. As firstly pointed out in,^[1] the slot waveguide can be used to greatly increase the sensitivity of compact optical sensing devices ^{[18][19][20][21][22][23][24]} or to enhance the efficiency of near-field optics probes.At Terahertz frequencies, slot waveguide based splitter has been designed which allows for low loss propagation of Terahertz waves. The device acts as a splitter through which maximum throughput can be achieved by adjusting the arm length ratio of the input to the output side.^[25]

References[edit]

1. ^ ^abcAlmeida, Vilson R.; Xu, Qianfan; Barrios, Carlos A.; Lipson, Michal (2004-06-01). 'Guiding and confining light in void nanostructure'. Optics Letters. The Optical Society. 29 (11): 1209–11. doi:10.1364/ol.29.001209. ISSN0146-9592. PMID15209249.
2. ^ ^abXu, Qianfan; Almeida, Vilson R.; Panepucci, Roberto R.; Lipson, Michal (2004-07-15). 'Experimental demonstration of guiding and confining light in nanometer-size low-refractive-index material'. Optics Letters. The Optical Society. 29 (14): 1626–8. doi:10.1364/ol.29.001626. ISSN0146-9592. PMID15309840.
3. ^Feng, N.-N.; Michel, J.; Kimerling, L.C. (2006). 'Optical Field Concentration in Low-Index Waveguides'. IEEE Journal of Quantum Electronics. Institute of Electrical and Electronics Engineers (IEEE). 42 (9): 883–888. doi:10.1109/jqe.2006.880061. ISSN0018-9197. S2CID46700811.
4. ^Sun, Rong; Dong, Po; Feng, Ning-ning; Hong, Ching-yin; Michel, Jurgen; Lipson, Michal; Kimerling, Lionel (2007). 'Horizontal single and multiple slot waveguides: optical transmission at λ = 1550 nm'. Optics Express. The Optical Society. 15 (26): 17967–72. doi:10.1364/oe.15.017967. ISSN1094-4087. PMID19551093.
5. ^Nagel, Michael; Marchewka, Astrid; Kurz, Heinrich (2006). 'Low-index discontinuity terahertz waveguides'. Optics Express. The Optical Society. 14 (21): 9944–54. doi:10.1364/oe.14.009944. ISSN1094-4087. PMID19529388.
6. ^ ^abBaehr-Jones, T.; Hochberg, M.; Wang, Guangxi; Lawson, R.; Liao, Y.; Sullivan, P. A.; Dalton, L.; Jen, A. K.-Y.; Scherer, A. (2005). 'Optical modulation and detection in slotted Silicon waveguides'. Optics Express. The Optical Society. 13 (14): 5216–26. doi:10.1364/opex.13.005216. ISSN1094-4087. PMID19498512.
7. ^Baehr-Jones, Tom; Penkov, Boyan; Huang, Jingqing; Sullivan, Phil; Davies, Joshua; et al. (2008-04-21). 'Nonlinear polymer-clad silicon slot waveguide modulator with a half wave voltage of 0.25V'. Applied Physics Letters. AIP Publishing. 92 (16): 163303. doi:10.1063/1.2909656. ISSN0003-6951.
8. ^Witzens, Jeremy; Baehr-Jones, Thomas; Hochberg, Michael (2010-07-26). 'Design of transmission line driven slot waveguideMach-Zehnder interferometers and application to analog optical links'. Optics Express. The Optical Society. 18 (16): 16902–28. doi:10.1364/oe.18.016902. ISSN1094-4087. PMID20721082.
9. ^ ^abWiederhecker, G. S.; Cordeiro, C. M. B.; Couny, F.; Benabid, F.; Maier, S. A.; et al. (2007). 'Field enhancement within an optical fibre with a subwavelength air core'. Nature Photonics. Springer Science and Business Media LLC. 1 (2): 115–118. doi:10.1038/nphoton.2006.81. ISSN1749-4885.
10. ^Haldar, Raktim; Mishra, V; Dutt, Avik; Varshney, Shailendra K (2016-09-09). 'On-chip broadband ultra-compact optical couplers and polarization splitters based on off-centered and non-symmetric slotted Si-wire waveguides'. Journal of Optics. IOP Publishing. 18 (10): 105801. doi:10.1088/2040-8978/18/10/105801. ISSN2040-8978.
11. ^Al-Tarawni, Musab A. M.; Bakar, A. Ashrif A.; Zain, Ahmad Rifqi Md.; Tarawneh, Mou’ad A.; Ahmad, Sahrim Hj. (2019-02-08). 'Enhancing the performance of strip and 180-deg slot waveguide bends for integrated optical waveguide modulator'. Optical Engineering. SPIE-Intl Soc Optical Eng. 58 (2): 027104. doi:10.1117/1.oe.58.2.027104. ISSN0091-3286. S2CID126965871.
12. ^Baehr-Jones, Tom; Hochberg, Michael; Walker, Chris; Scherer, Axel (2005-02-21). 'High-Q optical resonators in silicon-on-insulator-based slot waveguides'. Applied Physics Letters. AIP Publishing. 86 (8): 081101. doi:10.1063/1.1871360. ISSN0003-6951.
13. ^Schrauwen J., Van Lysebettens J., Vanhoutte M., Van Thourhout D. et al., 'Iodine enhanced focused ion beam etching of silicon for photonic device modification and prototyping (2008)', International Workshop on FIB for Photonics, 1st, Proceedings (2008)
14. ^Barrios, C. A.; Sánchez, B.; Gylfason, K. B.; Griol, A.; Sohlström, H.; Holgado, M.; Casquel, R. (2007). 'Demonstration of slot-waveguide structures on silicon nitride / silicon oxide platform'. Optics Express. The Optical Society. 15 (11): 6846–56. doi:10.1364/oe.15.006846. ISSN1094-4087. PMID19546997.
15. ^Barrios, C.A. (2004). 'High-performance all-optical silicon microswitch'. Electronics Letters. Institution of Engineering and Technology (IET). 40 (14): 862-863. doi:10.1049/el:20045179. ISSN0013-5194.
16. ^Barrios, Carlos Angulo; Lipson, Michal (2005). 'Electrically driven silicon resonant light emitting device based on slot-waveguide'. Optics Express. The Optical Society. 13 (25): 10092–101. doi:10.1364/opex.13.010092. ISSN1094-4087. PMID19503222.
17. ^A. Armaroli, A. Morand, P. Benech, G. Bellanca, S. Trillo, 'Comparative Analysis of a Planar Slotted Microdisk Resonator,' Lightwave Technology, Journal of , vol.27, no.18, pp.4009,4016, Sept.15, 2009
18. ^Barrios, Carlos Angulo (2006). 'Ultrasensitive Nanomechanical Photonic Sensor Based on Horizontal Slot-Waveguide Resonator'. IEEE Photonics Technology Letters. Institute of Electrical and Electronics Engineers (IEEE). 18 (22): 2419–2421. doi:10.1109/lpt.2006.886824. ISSN1041-1135. S2CID32069322.
19. ^Barrios, Carlos A.; Gylfason, Kristinn B.; Sánchez, Benito; Griol, Amadeu; Sohlström, H.; Holgado, M.; Casquel, R. (2007-10-17). 'Slot-waveguide biochemical sensor'. Optics Letters. The Optical Society. 32 (21): 3080–2. doi:10.1364/ol.32.003080. ISSN0146-9592. PMID17975603.
20. ^Dell'Olio, Francesco; Passaro, Vittorio M. (2007). 'Optical sensing by optimized silicon slot waveguides'. Optics Express. The Optical Society. 15 (8): 4977–93. doi:10.1364/oe.15.004977. ISSN1094-4087. PMID19532747.
21. ^Barrios, Carlos A.; Bañuls, María José; González-Pedro, Victoria; Gylfason, Kristinn B.; Sánchez, Benito; et al. (2008-03-28). 'Label-free optical biosensing with slot-waveguides'. Optics Letters. The Optical Society. 33 (7): 708–10. doi:10.1364/ol.33.000708. ISSN0146-9592. PMID18382525.
22. ^Robinson, Jacob T.; Chen, Long; Lipson, Michal (2008-03-13). 'On-chip gas detection in silicon optical microcavities'. Optics Express. The Optical Society. 16 (6): 4296–301. doi:10.1364/oe.16.004296. ISSN1094-4087. PMID18542525.
23. ^Witzens, Jeremy; Hochberg, Michael (2011-03-29). 'Optical detection of target molecule induced aggregation of nanoparticles by means of high-Q resonators'. Optics Express. The Optical Society. 19 (8): 7034–61. doi:10.1364/oe.19.007034. ISSN1094-4087. PMID21503017.
24. ^Ghosh, Souvik; Rahman, B. M. A. (2017). 'An Innovative Straight Resonator Incorporating a Vertical Slot as an Efficient Bio-Chemical Sensor'(PDF). IEEE Journal of Selected Topics in Quantum Electronics. Institute of Electrical and Electronics Engineers (IEEE). 23 (2): 132–139. doi:10.1109/jstqe.2016.2630299. ISSN1077-260X. S2CID10903140.
25. ^Pandey, Shashank; Kumar, Gagan; Nahata, Ajay (2010-10-22). 'Slot waveguide-based splitters for broadband terahertz radiation'. Optics Express. The Optical Society. 18 (22): 23466–71. doi:10.1364/oe.18.023466. ISSN1094-4087. PMID21164689.

Slot Antenna

Figure 1: The length of a slot determines the resonant frequency, the width of the slit determines the broad bandwidth of the slot radiator.

Figure 1: The length of a slot determines the resonant frequency, the width of the slit determines the broad bandwidth of the slot radiator.

Slot Antenna

Slot radiators orslot antennas are antennas that are used in the frequency range from about 300 MHz to 25 GHz. They are often used in navigation radar usually as an array fed by a waveguide. But also older large phased array antennas used the principle because the slot radiators are a very inexpensive way for frequency scanning arrays. Slot antennas are an about λ/2 elongated slot, cut in a conductive plate (Consider an infinite conducting sheet), and excited in the center. This slot behaves according to Babinet's principle as resonant radiator. Jacques Babinet (1794 - 1872) was a French physicist and mathematician, formulated the theorem that similar diffraction patterns are produced by two complementary screens (Babinet's principle). This principle relates the radiated fields and impedance of an aperture or slot antenna to that of the field of a dipole antenna. The polarization of a slot antenna is linear. The fields of the slot antenna are almost the same as the dipole antenna, but the field’s components are interchanged: a vertical slot has got an horizontal electric field; and the vertical dipole has got a vertical electrical field.

The impedance of the slot antenna (Z_s) is related to the impedance of its complementary dipole antenna (Z_d) by the relation:

It follows for Z_s = 485 Ω.

The band width of a narrow rectangular slot is equal to that of the related dipole, and is equal to half the bandwidth of a cylindrical dipole with a diameter equal to the slot width. Figure 2 shows slot antennas different from the rectangular shape that increasing the bandwidth of the slot antenna.

Figure 2: Various broadband slot antenna.

Although the theory requires an infinite spread conductive surface, the deviation from the theoretical value is small when the surface is greater than the square of the wavelength. The feeding of the slot antenna can be done with ordinary two-wire line. The impedance is dependent on the feeding point, as in a dipole. The value of 485 Ω applies only to a feeding point at the center. A shift of the feed point from the center to the edge steadily decreases the impedance.

The application of slot antennas can be versatile. They can replace dipoles e.g. if it is required a polarization perpendicular to the longitudinal extension of the radiator. If a dipole is used for feeding of a parabolic antenna to generate a vertically orientated but horizontally polarized fan beam, then this dipole must be orientated horizontally. This would mean that the edge surfaces of the parabolic reflector will not be sufficiently illuminated, but a lot of energy above and below the reflector would be lost. In addition, the length of the dipole is extended in a plane, in which is demanding a point like source of radiation for the focus of the parabolic reflector. If this dipole is replaced by a slot antenna, in this case don't appear these disadvantages.

Slots in waveguides

Figure 3: Various slot arrangements in a waveguide.

Figure 3: Various slot arrangements in a waveguide.

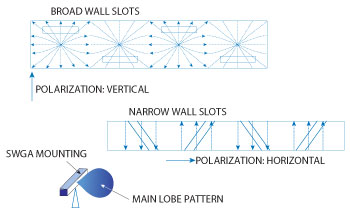
Slot antennas in waveguides provide an economical way of the design of antenna arrays. The position, shape and orientation of the slots will determine how (or if) they radiate. Figure 3 shows a rectangular waveguide with a drawn with red lines snapshot of the schematic current distribution in the waveguide walls. If slots are cut into the walls, so the current flow is affected more or less depending on the location of the slot. If the slots are sufficiently narrow so the slots B and C (Fig. 3) have little influence on the current distribution. These two slots radiate not (or very little). The slots A and D represent barriers to the current flow. Thus, this current flow acts as an excitation system for the slot, this one acts as radiator. Since the wave in the waveguide moves forward, these drawn lines migrate in the direction of propagation. The slot gets one always alternating voltage potential at its slot edges (depending on the frequency in the waveguide). The power that the slot radiates can be altered by moving the slots closer or farther from the edge. The slots A and D (as drawn in Figure 3) have the strongest coupling to the RF energy transported in the waveguide. In order to reduce this coupling, for example the slot A could be moved closer to one of the shorter waveguide walls. Rotating of the slots would have a the same effect (an angle between the orientations of A and B or C and D). The coupling of this rotated slot ist a factor of about sin² of the rotating angle θ.

Slotted Waveguide Antennas

Figure 4: Basic geometry of a slotted waveguide antenna (The slot radiators are on the wider wall of the rectangular waveguide.)

Rectangular Waveguide Tm Mode

Figure 4: Basic geometry of a slotted waveguide antenna (The slot radiators are on the wider wall of the rectangular waveguide.)

Circular Waveguide Modes

Several slot radiators in a waveguide form a group antenna. The waveguide is used as the transmission line to feed the elements. In order for radiate in the correct phase, all single slots must be cutted in the distance of the wavelength, that is valid for the interior of the waveguide. This wavelength differs from the wavelength in free space and is a function of the wider side a of a rectangular waveguide. Usually this wavelength is calculated for the TE₁₀ mode by:

Slab Waveguide Mode Calculator

a = length of the wider side of the rectangular waveguides
λ_h = “guided” wavelength (within the waveguide)
λ = wavelength in free space(2)

Silicon Slot Waveguide

Figure 5: Basic geometry of a slotted waveguide antenna with rotated slot antennas on the narrower wall.

Figure 5: Basic geometry of a slotted waveguide antenna with rotated slot antennas on the narrower wall.

The wavelength within the waveguide is longer than in free space. The distance of the slot radiators in the group is set at this wavelength to a value that is slightly larger than the wavelength λ in the free space. The number and the size of the sidelobes is affected so unfavorably. The slots are often attached to the left and right eccentrically (with reduced coupling). If mounted on the narrow side of the waveguide, it may happen that the length for the resonant slot radiator is shorter than the wall. In this case, the slot can be also guided around the corners, it then lies also slightly on the A-side of the waveguide. In practice, these slots are all covered with a thin insulating material (for the protection of the interior) of the waveguide. This material may not be hygroscopic and must be protected from weather conditions.

A single narrow slot radiator can also work on frequencies ±5 … ±10% besides its resonance frequency. For array antennas, this is not possible so easily. Such a group antenna is fixed strongly to a single frequency, which is determined by the spacing of exactly λ_h, and for which the antenna has been optimized. If the frequency is changed, then these distances not correct, the performance of the antenna decreases. The phase difference arising between the antenna elements are added to the whole length of the antenna to values ​​that can no longer be tolerated. This antenna begins to “squint”, that is, the antenna pattern points in a different direction from the optical center axis. This effect can also be exploited to achieve an electronic pivoting of the antenna beam as a function of change of the transmission frequency.